Forum Links
Three Things to Remember
Trigonometry, the Study of Triangles [Math]
Trigonometry, the Study of Triangles [Math]
Related Threads
Coming Soon
Thread Information
Thread Actions
Thread Closed

New Thread

New Poll

Order
Three Things to Remember
04-13-14 11:13 AM
 Singelli is Offline
| ID: 1006942 | 2702 Words
Singelli is Offline
| ID: 1006942 | 2702 Words
 Singelli is Offline
Singelli is Offline
| ID: 1006942 | 2702 Words
Singelli
Level: 164





POSTS: 6573/8698
POST EXP: 1189395
LVL EXP: 56733091
CP: 67403.0
VIZ: 3154373

POSTS: 6573/8698
POST EXP: 1189395
LVL EXP: 56733091
CP: 67403.0
VIZ: 3154373

Likes: 1 Dislikes: 0
This thread will discuss the nuances of trigonometry, the study of triangles. As with my other threads, I will create videos to go along with the lesson. The first video I made, however, ended up having bad quality, and I'm not quite sure why. I tried making an actual video of myself writing on paper taped to my wall, because recording my screen while using Paint is not very easy to do. If any of you have seen my old videos and watch the new ones, can you tell me which you prefer? For these trig videos, the image ended up being a little small, and the sound quips out frequently for seconds at a time. Actually, I just kept watching it, and it gets worse as the time moves along. :/ I'm going to link these for now, but the lag becomes pretty bad. I'll What exactly is Trigonometry? Trigonometry quite literally translates into 'the study of triangles'. Although any type of triangles can be studied, the most basic of trigonometry focuses on right triangles: those with one 90 degree angle. Due to the way triangles are 'built', certain values may be calculable, such as the side length or angle. This becomes important especially in the fields of architecture and engineering when certain heights or slopes of structures are needed. The First Thing to Know Much of basic trigonometry can be done with very limited knowledge. The first thing you should know about a triangle's structure is that every angle combined adds to 180 degrees. In other words, if one angle is 100 degrees and a second angle is 50 degrees, then the last angle MUST be 30 degrees, since that would bring their total to 180 degrees. This is essential to know for many reasons and will become a very useful fact as you move along towards more difficult problems. Since the most basic trigonometry deals with right triangles, knowing the 'Triangle Sum Property' also helps us gain more information. If one of the angles is 90 degrees, that means the other two angles must also add to be 90 degrees (because 90 + 90 is 180). Therefore, in a right triangle, if one angle is 30 degrees, the last angle will be 60 degrees. If one angle is 81 degrees, the last angle will be 9 degrees. Using the same logic, it should be pretty clear that it is impossible for a triangle to have more than one right angle. Just as the Triangle Sum Property can be used to find a missing angle, the Pythagorean Theorem can be used to find a missing side. In case you don't know what the Pythagorean Theorem is, it's a formula that can ONLY be used in right triangles, and it looks like this: a2 + b2 = c2. a and b represent any two sides of the triangle other than the hypotenuse (see the section below if you don't know the meaning of hypotenuse), while c MUST be the hypotenuse. Let's say for example, that you had a triangle like the one below (answers.tutorvista.com).  In this image, the side labeled 'c' is the hypotenuse and should take the place of 'c' in the Pythagorean Theorem.Thus, your work would look like this: 52 + 42 = c2 25 + 16 = c2 41 = c2 (To Solve this, take the square root of both sides) c ≈ 6.4 The Second Thing to Know Since trigonometry focuses on the ratios of triangle sides, it'd be pretty impossible to get far unless we identify the sides first. If we can't agree on which sides to use, then we can't feasibly work together and get the same answers. Therefore, all triangles sides will be recognized as the hypotenuse, the opposite side, or the adjacent side. The hypotenuse is quite likely the easiest to recognize, as it's always across from the 90 degree angle and is also the longest side. This image from wikipedia can give you a better idea of what I mean: 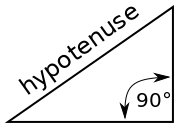 The hypotenuse does not change no matter what angle is being focused on. That can't be said for the other two sides. In order to recognize which side is 'opposite', for example, you'll need to know what it's opposite from. Therefore, you must have an angle of focus. Most of the time, this angle is labeled with the symbol, theta, which looks like this: θ. It's the ninth letter of the Greek alphabet, lower case. Whenever you see this symbol, you will know to identify the other sides in relation to THAT angle. Some students have trouble recognizing which side is across from an angle. To make this a little easier, I often tell my students to imagine theta is a flashlight head. If the flashlight were turned on, where would the light strike? This is the opposite side. Once you have the hypotenuse recognized, and the opposite side, the last side MUST be the adjacent side. Here is a wonderful image from www.mathisfun.com: 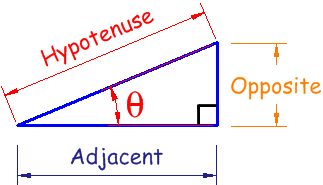 (As a side note, the square in the lower right corner signifies a 90 degree angle.) Once you can easily label the three sides, you can then move on to studying the three trig functions themselves. The Third Thing to Know Once you understand the Triangle Sum Property and you're easily able to identify the three sides of a triangle, you're ready to tackle the trigonometric ratios. There are six ratios overall, but only three of them are absolutely necessary. They are called sine, cosine, and tangent. You could honestly even get by with only sine and cosine, since all other trig functions can be found using just those two. Most of the time, you see these three trig functions abbreviated using their first three letters; in other words, in your books and on your calculator, they appear to be 'sin', 'cos', and 'tan'. As you progress through the study of triangles, one simple fact can keep you from screwing up more difficult problems. Remember that 'sin', 'cos', and 'tan' make NO sense without a value attached to them. Let me put it to you this way: If I gave you a square root symbol, but I placed no number underneath, would you be able to give me a solution? The answer of course... is no. A square root symbol only makes sense if I put a number underneath it. If, for example, I wrote a square root symbol and wrote a 25 underneath, your brain could then process that I'm asking you to find what number multiplied by itself will give you 25. In the same way that a square root doesn't make sense without a number attached, a trig function does not make sense without an angle attached. You should never see 'sin' all by itself. Instead, you might see sinθ, sinA, or sin34°. Whatever is attached to the trig function MUST be an angle. Each trig function has a formula. They are as follows: sinθ = opp hyp cosθ = adj hyp tanθ = opp hyp Since these might be difficult to remember, I suggest using an acronym or mnemonic device. The most commonly used one is SOHCAHTOA. (Try saying "Some Of His Children Are Having Trouble Over Algebra" if you can't remember how to spell it.) This word basically uses the first letter of each function and then the first letter of each part of its matching formula: S = sine is O = opposite over H = hypotenuse. C = cosine is A = adjacent over H = hypotenuse. T = tangent is O = opposite over A = adjacent. What to do with this Information. Okay, so if you can master the three concepts above and you have a decent understanding of algebra, you can work basic trig problems. The foundation of all problems is being able to calculate the three trig ratios. For example, take a look at this image I stole from math.tutorvista.com:  If I ask you to find sinC, cosC, and tanC (read it as "sine OF C", "cosine OF C", "tangent OF C"), you should be able to apply the formulas above. sinC = opp = 3 hyp 5 cosC = adj = 4 hyp 5 tanC = opp = 3 hyp 4 If you're not sure how to get this, try first labeling each side of the triangle as hypotenuse, opposite, or adjacent. What exactly do these fractions mean? Well, let's look at the sine ratio. The formula is opposite over hypotenuse, and we got 3/5. Translated into a decimal, 3/5 is 0.6, which is equivalent to 60%. In other words, in any triangle with matching angles, the opposite side will be 60% the size of the hypotenuse. Another triangle, for example, might have the exact same angles, but side lengths of 6, 8, and 10. If you were to compare the opposite side with the hypotenuse, the opposite side (6) would be 60% of the hypotenuse (10). This may be slightly above your head, and if so, don't fret about it. It's not crucial to being able to work problems. For now, why don't you try finding the three trig functions for this problem taken from karen.mcnabbs.org. Use angle B as your theta. I have provided the answers in a spoiler below. 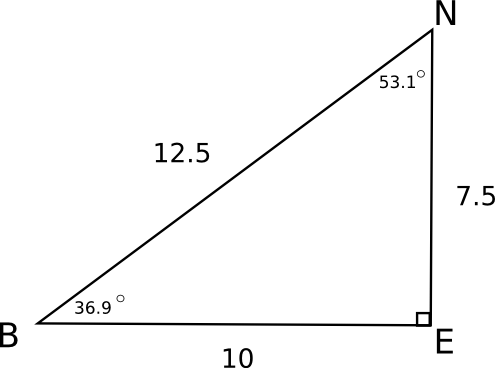 Spoiler: sinB = opp = 7.5 hyp 12.5 cosB = adj = 10 hyp 12.5 tanB = opp = 7.5 hyp 10 Sometimes problems aren't as simple as these ones are. Let's take a look at a problem from www.ck12.org. Do you notice anything different about it? Hopefully, you at least noticed that the problem is missing a side. If this happens, don't fret! We always have the Pythagorean Theorem on our side. This just means that we can't find the three trig functions without a little work beforehand. In this case, we don't KNOW the hypotenuse, so 'a' and 'b' can be 5 and 8, whereas 'c' will be our goal. 52 + 82 = c2 25 + 64 = c2 89 = c2 c ≈ 9.4 Now that we have all three sides, we can attempt to find the three ratios. Once again, I will place the answers in a spoiler for you. Try finding all three ratios for angle C. Spoiler: sinC = opp = 5 hyp 9.4 cosC = adj = 8 hyp 9.4 tanC = opp = 5 hyp 8 Delving a Little Deeper Alright, so most likely, you're wondering what the purpose is in listing a bunch of fractions. Truth be told, simply listing the fractions is not a very useful skill when it comes to building a bridge or designing the inside framework of a roof. However, having the skill to list the fractions DOES allow us to work much more complicated problems. Take the following problem as an example (taken from wmich.edu):  Although this problem looks nothing like the other ones we have seen, we now have all the knowledge necessary for completing the problem. That is, we are capable of finding the value of 'a'. First, take a look at what information is given. We have the angle A (43 degrees) and two sides of the triangle ('a' and 11). The important question is this: WHICH sides of the triangle are 'a' and 11? Since 43 degrees is the angle given to us, we can assume it is our theta. (Never, ever use the 90 degree angle to solve these types of problems. It won't work, because then the hypotenuse IS the opposite side.) If angle A is our theta, this makes 'a' our opposite side, and 11 must be the adjacent side. Now ask yourself the following question: which ratio uses opposite and adjacent? The answer, of course, is the tangent function. You should be able to fill it in with all the appropriate information. tanθ = opp hyp So: tan43°= a 11 Solving such a problem is then a matter of basic algebra. If I want to get 'a' by itself, I have to note that 'a' is being divided by 11. The opposite of division is multiplication, so I have to multiply 11 to both sides. Doing so will leave me with: 11tan43° = a This is something you can plug directly into your calculator. Doing so will give you the answer of about 10.3. If you don't get 10.3, that's because your calculator is in the wrong mode, and you'll have to change that. You can learn how to change the mode of your calculator by googling the instructions, as it would take far too long for me to go over every possible calculator model you might have. However, do be sure that your calculator is in 'degree' mode and not 'radian' mode. Let's try another problem. This one comes from cimt.plymouth.ac.uk.  In this problem, our theta is 50 degrees. 8 is the hypotenuse since it is across from the right angle, and 'y' must be the adjacent side, because it's right next to the 50 degrees. Therefore, we'll be using the cosine ratio, because it's the only trig function we know about that uses adjacent and hypotenuse. Since we know this, we can begin to fill in our problem. cosθ = adj hyp so cos50°= y 8 We can then multiply 8 to the other side of the equation, which gives us 8cos50° = y. Plugging this into our calculator gives us about 5.1. Some problems may cause more issue... especially for students who struggle with algebra. Take, for example, this problem from www.softschools.com: 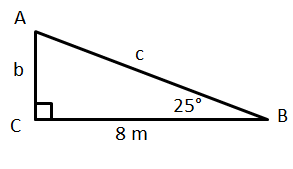 Let's solve for 'c' and ignore the 'b'. We can find both, but I just want to find 'c'. Alright, so in this problem, we are given the angle (25 degrees), the hypotenuse ('c'), and the adjacent side (8). If we want to figure out the value of 'c', we will need to use cosine again because we have the adjacent side and the hypotenuse. You should be able to fill the formula in with no problem. cosθ = adj hyp so cos25°= 8 c This time, the variable is in the denominator. There are several ways to resolve the issue, but the fact of the matter is that this problem can NOT be solved by multiplying 8 to the other side. Eight is not in the denominator. Although there are many methods for solving this, I suggest the following: Whenever you see a fraction that you need to break up, ALWAYS multiply whatever is in the denominator to both sides of the equation. In this particular problem, the denominator is c. If you multiply c to both sides, you'll get the following: c cos25° = 8 The problem still isn't solved because you want to have 'c' all by it's lonesome self, and it has this pesky trig function attached to it. Remember this though: a trig function does NOT make sense without its attached angle. Therefore, that 'cos' and that '25' MUST STICK TOGETHER AT ALL COSTS. Treat cos25° like any other number. After all, if you plugged it into the calculator, you'd get a decimal value. What does this mean? This means we have c cos25°, or c TIMES a number. How do you get rid of that number? Well, the opposite of multiplication is division, so you must divide cos25° to the other side of the equation. Thus, what you really get is this: c cos25° = 8 cos25° cos25° or c = 8 cos25° Plug this into your calculator and you come up with about 8.8. ----------------------------- I'm sure by now your head hurts, so I'm going to leave it at that. Once you've had time to practice a few problems (just google them, seriously!), I'll continue on with the lesson. Kuta software is always a wonderful site to get practice problems from. Just look for "Solving Trig Ratios". Good luck, and God bless! If you have any questions, feel free to post them here! Actually, I just kept watching it, and it gets worse as the time moves along. :/ I'm going to link these for now, but the lag becomes pretty bad. I'll What exactly is Trigonometry? Trigonometry quite literally translates into 'the study of triangles'. Although any type of triangles can be studied, the most basic of trigonometry focuses on right triangles: those with one 90 degree angle. Due to the way triangles are 'built', certain values may be calculable, such as the side length or angle. This becomes important especially in the fields of architecture and engineering when certain heights or slopes of structures are needed. The First Thing to Know Much of basic trigonometry can be done with very limited knowledge. The first thing you should know about a triangle's structure is that every angle combined adds to 180 degrees. In other words, if one angle is 100 degrees and a second angle is 50 degrees, then the last angle MUST be 30 degrees, since that would bring their total to 180 degrees. This is essential to know for many reasons and will become a very useful fact as you move along towards more difficult problems. Since the most basic trigonometry deals with right triangles, knowing the 'Triangle Sum Property' also helps us gain more information. If one of the angles is 90 degrees, that means the other two angles must also add to be 90 degrees (because 90 + 90 is 180). Therefore, in a right triangle, if one angle is 30 degrees, the last angle will be 60 degrees. If one angle is 81 degrees, the last angle will be 9 degrees. Using the same logic, it should be pretty clear that it is impossible for a triangle to have more than one right angle. Just as the Triangle Sum Property can be used to find a missing angle, the Pythagorean Theorem can be used to find a missing side. In case you don't know what the Pythagorean Theorem is, it's a formula that can ONLY be used in right triangles, and it looks like this: a2 + b2 = c2. a and b represent any two sides of the triangle other than the hypotenuse (see the section below if you don't know the meaning of hypotenuse), while c MUST be the hypotenuse. Let's say for example, that you had a triangle like the one below (answers.tutorvista.com).  In this image, the side labeled 'c' is the hypotenuse and should take the place of 'c' in the Pythagorean Theorem.Thus, your work would look like this: 52 + 42 = c2 25 + 16 = c2 41 = c2 (To Solve this, take the square root of both sides) c ≈ 6.4 The Second Thing to Know Since trigonometry focuses on the ratios of triangle sides, it'd be pretty impossible to get far unless we identify the sides first. If we can't agree on which sides to use, then we can't feasibly work together and get the same answers. Therefore, all triangles sides will be recognized as the hypotenuse, the opposite side, or the adjacent side. The hypotenuse is quite likely the easiest to recognize, as it's always across from the 90 degree angle and is also the longest side. This image from wikipedia can give you a better idea of what I mean:  The hypotenuse does not change no matter what angle is being focused on. That can't be said for the other two sides. In order to recognize which side is 'opposite', for example, you'll need to know what it's opposite from. Therefore, you must have an angle of focus. Most of the time, this angle is labeled with the symbol, theta, which looks like this: θ. It's the ninth letter of the Greek alphabet, lower case. Whenever you see this symbol, you will know to identify the other sides in relation to THAT angle. Some students have trouble recognizing which side is across from an angle. To make this a little easier, I often tell my students to imagine theta is a flashlight head. If the flashlight were turned on, where would the light strike? This is the opposite side. Once you have the hypotenuse recognized, and the opposite side, the last side MUST be the adjacent side. Here is a wonderful image from www.mathisfun.com:  (As a side note, the square in the lower right corner signifies a 90 degree angle.) Once you can easily label the three sides, you can then move on to studying the three trig functions themselves. The Third Thing to Know Once you understand the Triangle Sum Property and you're easily able to identify the three sides of a triangle, you're ready to tackle the trigonometric ratios. There are six ratios overall, but only three of them are absolutely necessary. They are called sine, cosine, and tangent. You could honestly even get by with only sine and cosine, since all other trig functions can be found using just those two. Most of the time, you see these three trig functions abbreviated using their first three letters; in other words, in your books and on your calculator, they appear to be 'sin', 'cos', and 'tan'. As you progress through the study of triangles, one simple fact can keep you from screwing up more difficult problems. Remember that 'sin', 'cos', and 'tan' make NO sense without a value attached to them. Let me put it to you this way: If I gave you a square root symbol, but I placed no number underneath, would you be able to give me a solution? The answer of course... is no. A square root symbol only makes sense if I put a number underneath it. If, for example, I wrote a square root symbol and wrote a 25 underneath, your brain could then process that I'm asking you to find what number multiplied by itself will give you 25. In the same way that a square root doesn't make sense without a number attached, a trig function does not make sense without an angle attached. You should never see 'sin' all by itself. Instead, you might see sinθ, sinA, or sin34°. Whatever is attached to the trig function MUST be an angle. Each trig function has a formula. They are as follows: sinθ = opp hyp cosθ = adj hyp tanθ = opp hyp Since these might be difficult to remember, I suggest using an acronym or mnemonic device. The most commonly used one is SOHCAHTOA. (Try saying "Some Of His Children Are Having Trouble Over Algebra" if you can't remember how to spell it.) This word basically uses the first letter of each function and then the first letter of each part of its matching formula: S = sine is O = opposite over H = hypotenuse. C = cosine is A = adjacent over H = hypotenuse. T = tangent is O = opposite over A = adjacent. What to do with this Information. Okay, so if you can master the three concepts above and you have a decent understanding of algebra, you can work basic trig problems. The foundation of all problems is being able to calculate the three trig ratios. For example, take a look at this image I stole from math.tutorvista.com:  If I ask you to find sinC, cosC, and tanC (read it as "sine OF C", "cosine OF C", "tangent OF C"), you should be able to apply the formulas above. sinC = opp = 3 hyp 5 cosC = adj = 4 hyp 5 tanC = opp = 3 hyp 4 If you're not sure how to get this, try first labeling each side of the triangle as hypotenuse, opposite, or adjacent. What exactly do these fractions mean? Well, let's look at the sine ratio. The formula is opposite over hypotenuse, and we got 3/5. Translated into a decimal, 3/5 is 0.6, which is equivalent to 60%. In other words, in any triangle with matching angles, the opposite side will be 60% the size of the hypotenuse. Another triangle, for example, might have the exact same angles, but side lengths of 6, 8, and 10. If you were to compare the opposite side with the hypotenuse, the opposite side (6) would be 60% of the hypotenuse (10). This may be slightly above your head, and if so, don't fret about it. It's not crucial to being able to work problems. For now, why don't you try finding the three trig functions for this problem taken from karen.mcnabbs.org. Use angle B as your theta. I have provided the answers in a spoiler below.  Spoiler: sinB = opp = 7.5 hyp 12.5 cosB = adj = 10 hyp 12.5 tanB = opp = 7.5 hyp 10 Sometimes problems aren't as simple as these ones are. Let's take a look at a problem from www.ck12.org. Do you notice anything different about it? Hopefully, you at least noticed that the problem is missing a side. If this happens, don't fret! We always have the Pythagorean Theorem on our side. This just means that we can't find the three trig functions without a little work beforehand. In this case, we don't KNOW the hypotenuse, so 'a' and 'b' can be 5 and 8, whereas 'c' will be our goal. 52 + 82 = c2 25 + 64 = c2 89 = c2 c ≈ 9.4 Now that we have all three sides, we can attempt to find the three ratios. Once again, I will place the answers in a spoiler for you. Try finding all three ratios for angle C. Spoiler: sinC = opp = 5 hyp 9.4 cosC = adj = 8 hyp 9.4 tanC = opp = 5 hyp 8 Delving a Little Deeper Alright, so most likely, you're wondering what the purpose is in listing a bunch of fractions. Truth be told, simply listing the fractions is not a very useful skill when it comes to building a bridge or designing the inside framework of a roof. However, having the skill to list the fractions DOES allow us to work much more complicated problems. Take the following problem as an example (taken from wmich.edu):  Although this problem looks nothing like the other ones we have seen, we now have all the knowledge necessary for completing the problem. That is, we are capable of finding the value of 'a'. First, take a look at what information is given. We have the angle A (43 degrees) and two sides of the triangle ('a' and 11). The important question is this: WHICH sides of the triangle are 'a' and 11? Since 43 degrees is the angle given to us, we can assume it is our theta. (Never, ever use the 90 degree angle to solve these types of problems. It won't work, because then the hypotenuse IS the opposite side.) If angle A is our theta, this makes 'a' our opposite side, and 11 must be the adjacent side. Now ask yourself the following question: which ratio uses opposite and adjacent? The answer, of course, is the tangent function. You should be able to fill it in with all the appropriate information. tanθ = opp hyp So: tan43°= a 11 Solving such a problem is then a matter of basic algebra. If I want to get 'a' by itself, I have to note that 'a' is being divided by 11. The opposite of division is multiplication, so I have to multiply 11 to both sides. Doing so will leave me with: 11tan43° = a This is something you can plug directly into your calculator. Doing so will give you the answer of about 10.3. If you don't get 10.3, that's because your calculator is in the wrong mode, and you'll have to change that. You can learn how to change the mode of your calculator by googling the instructions, as it would take far too long for me to go over every possible calculator model you might have. However, do be sure that your calculator is in 'degree' mode and not 'radian' mode. Let's try another problem. This one comes from cimt.plymouth.ac.uk.  In this problem, our theta is 50 degrees. 8 is the hypotenuse since it is across from the right angle, and 'y' must be the adjacent side, because it's right next to the 50 degrees. Therefore, we'll be using the cosine ratio, because it's the only trig function we know about that uses adjacent and hypotenuse. Since we know this, we can begin to fill in our problem. cosθ = adj hyp so cos50°= y 8 We can then multiply 8 to the other side of the equation, which gives us 8cos50° = y. Plugging this into our calculator gives us about 5.1. Some problems may cause more issue... especially for students who struggle with algebra. Take, for example, this problem from www.softschools.com:  Let's solve for 'c' and ignore the 'b'. We can find both, but I just want to find 'c'. Alright, so in this problem, we are given the angle (25 degrees), the hypotenuse ('c'), and the adjacent side (8). If we want to figure out the value of 'c', we will need to use cosine again because we have the adjacent side and the hypotenuse. You should be able to fill the formula in with no problem. cosθ = adj hyp so cos25°= 8 c This time, the variable is in the denominator. There are several ways to resolve the issue, but the fact of the matter is that this problem can NOT be solved by multiplying 8 to the other side. Eight is not in the denominator. Although there are many methods for solving this, I suggest the following: Whenever you see a fraction that you need to break up, ALWAYS multiply whatever is in the denominator to both sides of the equation. In this particular problem, the denominator is c. If you multiply c to both sides, you'll get the following: c cos25° = 8 The problem still isn't solved because you want to have 'c' all by it's lonesome self, and it has this pesky trig function attached to it. Remember this though: a trig function does NOT make sense without its attached angle. Therefore, that 'cos' and that '25' MUST STICK TOGETHER AT ALL COSTS. Treat cos25° like any other number. After all, if you plugged it into the calculator, you'd get a decimal value. What does this mean? This means we have c cos25°, or c TIMES a number. How do you get rid of that number? Well, the opposite of multiplication is division, so you must divide cos25° to the other side of the equation. Thus, what you really get is this: c cos25° = 8 cos25° cos25° or c = 8 cos25° Plug this into your calculator and you come up with about 8.8. ----------------------------- I'm sure by now your head hurts, so I'm going to leave it at that. Once you've had time to practice a few problems (just google them, seriously!), I'll continue on with the lesson. Kuta software is always a wonderful site to get practice problems from. Just look for "Solving Trig Ratios". Good luck, and God bless! If you have any questions, feel free to post them here! |
Vizzed Elite
Affected by 'Laziness Syndrome'
Registered: 08-09-12
Location: Alabama
Last Post: 3141 days
Last Active: 3116 days
| Singelli |
Affected by 'Laziness Syndrome'
Registered: 08-09-12
Location: Alabama
Last Post: 3141 days
Last Active: 3116 days
Post Rating: 1 Liked By: Mia03,
Links
Page Comments
This page has no comments


 User Notice
User Notice 